LoRA (adaptación de bajo rango) es una nueva técnica para ajustar modelos preentrenados a gran escala. Estos modelos suelen entrenarse con datos de dominio common, para tener la máxima cantidad de datos. Para obtener mejores resultados en tareas como chatear o responder preguntas, estos modelos se pueden “afinar” o adaptar aún más en datos específicos del dominio.
Es posible ajustar un modelo simplemente inicializándolo con los pesos previamente entrenados y entrenándolo más con los datos específicos del dominio. Con el tamaño cada vez mayor de los modelos previamente entrenados, un ciclo completo de avance y retroceso requiere una gran cantidad de recursos informáticos. El ajuste fino simplemente mediante capacitación continua también requiere una copia completa de todos los parámetros para cada tarea/dominio al que se adapta el modelo.
LoRA: adaptación de bajo rango de modelos de lenguaje grandes
propone una solución para ambos problemas mediante el uso de una descomposición matricial de bajo rango. Puede reducir la cantidad de pesos entrenables 10,000 veces y los requisitos de memoria de GPU 3 veces.
Método
El problema de ajustar una purple neuronal se puede expresar encontrando un (Delta Theta)
que minimiza (L(X, y; Theta_0 + DeltaTheta)) dónde (L) es una función de pérdida, (INCÓGNITA) y (y)
son los datos y (Theta_0) los pesos de un modelo previamente entrenado.
Aprendemos los parámetros. (Delta Theta) con dimensión (|Delta Theta|)
es igual a (|Theta_0|). Cuando (|Theta_0|) es muy grande, como en modelos pre-entrenados a gran escala, encontrar (Delta Theta) se vuelve computacionalmente desafiante. Además, para cada tarea es necesario aprender algo nuevo. (Delta Theta) conjunto de parámetros, lo que hace que sea aún más difícil implementar modelos ajustados si tiene más de unas pocas tareas específicas.
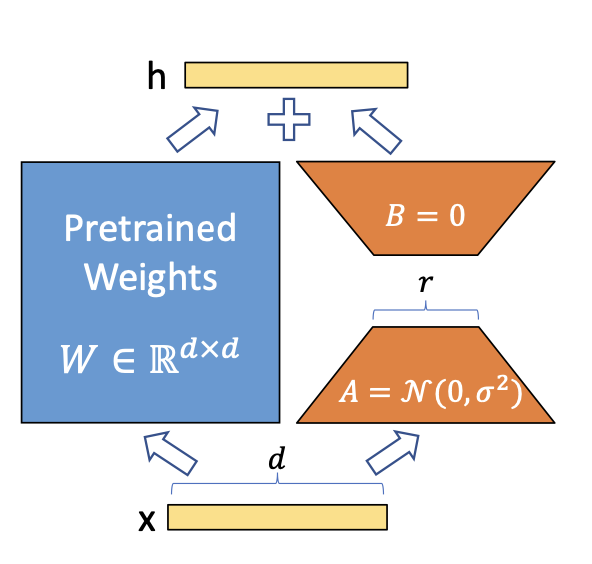
LoRA propone utilizar una aproximación (Delta Phi aprox Delta Theta) con (|Delta Phi| << |Delta Theta|). La observación es que las redes neuronales tienen muchas capas densas que realizan la multiplicación de matrices y, si bien normalmente tienen un rango completo durante el preentrenamiento, cuando se adaptan a una tarea específica las actualizaciones de peso tendrán una “dimensión intrínseca” baja.
Se aplica una descomposición matricial easy para cada actualización de la matriz de peso. (Delta theta en Delta Theta). En vista de (Delta theta_i in mathbb{R}^{d occasions okay}) la actualización para el (i)º peso en la purple, LoRA lo aproxima con:
[Delta theta_i approx Delta phi_i = BA]
dónde (B in mathbb{R}^{d occasions r}), (A in mathbb{R}^{r occasions d}) y el rango (r << mín(d, okay)). Así, en lugar de aprender (d veces okay) parámetros que ahora necesitamos aprender ((d + okay) veces r) que es fácilmente mucho más pequeño dado el aspecto multiplicativo. En la práctica, (Delta theta_i) es escalado por (frac{alpha}{r}) antes de ser agregado a (theta_i)que puede interpretarse como una “tasa de aprendizaje” para la actualización de LoRA.
LoRA no aumenta la latencia de inferencia, ya que una vez realizado el ajuste fino, simplemente puede actualizar los pesos en (Theta) añadiendo sus respectivos (Delta theta aprox Delta phi). También simplifica la implementación de múltiples modelos de tareas específicas sobre un modelo grande, como (|Delta Fi|) es mucho más pequeño que (|Delta Theta|).
Implementando en antorcha
Ahora que tenemos una thought de cómo funciona LoRA, implementémoslo usando antorcha para solucionar un problema mínimo. Nuestro plan es el siguiente:
- Simule datos de entrenamiento usando un easy (y = X theta) modelo. (theta in mathbb{R}^{1001, 1000}).
- Entrene un modelo lineal de rango completo para estimar (theta) – este será nuestro modelo ‘pre-entrenado’.
- Simule una distribución diferente aplicando una transformación en (theta).
- Entrene un modelo de rango bajo utilizando los pesos previamente entrenados.
Comencemos simulando los datos de entrenamiento:
Ahora definimos nuestro modelo base:
mannequin <- nn_linear(d_in, d_out, bias = FALSE)También definimos una función para entrenar un modelo, que también reutilizaremos más adelante. La función realiza el bucle de entrenamiento estándar en la antorcha utilizando el optimizador Adam. Los pesos del modelo se actualizan in situ.
practice <- operate(mannequin, X, y, batch_size = 128, epochs = 100) {
decide <- optim_adam(mannequin$parameters)
for (epoch in 1:epochs) {
for(i in seq_len(n/batch_size)) {
idx <- pattern.int(n, dimension = batch_size)
loss <- nnf_mse_loss(mannequin(X[idx,]), y[idx])
with_no_grad({
decide$zero_grad()
loss$backward()
decide$step()
})
}
if (epoch %% 10 == 0) {
with_no_grad({
loss <- nnf_mse_loss(mannequin(X), y)
})
cat("[", epoch, "] Loss:", loss$merchandise(), "n")
}
}
}Luego se entrena el modelo:
practice(mannequin, X, y)
#> [ 10 ] Loss: 577.075
#> [ 20 ] Loss: 312.2
#> [ 30 ] Loss: 155.055
#> [ 40 ] Loss: 68.49202
#> [ 50 ] Loss: 25.68243
#> [ 60 ] Loss: 7.620944
#> [ 70 ] Loss: 1.607114
#> [ 80 ] Loss: 0.2077137
#> [ 90 ] Loss: 0.01392935
#> [ 100 ] Loss: 0.0004785107Bien, ahora tenemos nuestro modelo base previamente entrenado. Supongamos que tenemos datos de una distribución ligeramente diferente que simulamos usando:
thetas2 <- thetas + 1
X2 <- torch_randn(n, d_in)
y2 <- torch_matmul(X2, thetas2)Si aplicamos nuestro modelo base a esta distribución, no obtenemos un buen rendimiento:
nnf_mse_loss(mannequin(X2), y2)
#> torch_tensor
#> 992.673
#> [ CPUFloatType{} ][ grad_fn = <MseLossBackward0> ]Ahora ajustamos nuestro modelo inicial. La distribución de los nuevos datos es ligeramente diferente a la inicial. Es solo una rotación de los puntos de datos, sumando 1 a todos los thetas. Esto significa que no se espera que las actualizaciones de peso sean complejas y no deberíamos necesitar una actualización de rango completo para obtener buenos resultados.
Definamos un nuevo módulo de antorcha que implemente la lógica LoRA:
lora_nn_linear <- nn_module(
initialize = operate(linear, r = 16, alpha = 1) {
self$linear <- linear
# parameters from the unique linear module are 'freezed', so they don't seem to be
# tracked by autograd. They're thought of simply constants.
purrr::stroll(self$linear$parameters, (x) x$requires_grad_(FALSE))
# the low rank parameters that might be educated
self$A <- nn_parameter(torch_randn(linear$in_features, r))
self$B <- nn_parameter(torch_zeros(r, linear$out_feature))
# the scaling fixed
self$scaling <- alpha / r
},
ahead = operate(x) {
# the modified ahead, that simply provides the consequence from the bottom mannequin
# and ABx.
self$linear(x) + torch_matmul(x, torch_matmul(self$A, self$B)*self$scaling)
}
)Ahora inicializamos el modelo LoRA. usaremos (r = 1)lo que significa que A y B serán solo vectores. El modelo base tiene parámetros entrenables de 1001×1000. El modelo LoRA que vamos a ajustar tiene solo (1001 + 1000), lo que lo convierte en 1/500 de los parámetros del modelo base.
lora <- lora_nn_linear(mannequin, r = 1)Ahora entrenemos el modelo lora en la nueva distribución:
practice(lora, X2, Y2)
#> [ 10 ] Loss: 798.6073
#> [ 20 ] Loss: 485.8804
#> [ 30 ] Loss: 257.3518
#> [ 40 ] Loss: 118.4895
#> [ 50 ] Loss: 46.34769
#> [ 60 ] Loss: 14.46207
#> [ 70 ] Loss: 3.185689
#> [ 80 ] Loss: 0.4264134
#> [ 90 ] Loss: 0.02732975
#> [ 100 ] Loss: 0.001300132 si miramos (Delta theta) veremos una matriz llena de unos, la transformación exacta que aplicamos a los pesos:
delta_theta <- torch_matmul(lora$A, lora$B)*lora$scaling
delta_theta[1:5, 1:5]
#> torch_tensor
#> 1.0002 1.0001 1.0001 1.0001 1.0001
#> 1.0011 1.0010 1.0011 1.0011 1.0011
#> 0.9999 0.9999 0.9999 0.9999 0.9999
#> 1.0015 1.0014 1.0014 1.0014 1.0014
#> 1.0008 1.0008 1.0008 1.0008 1.0008
#> [ CPUFloatType{5,5} ][ grad_fn = <SliceBackward0> ]Para evitar la latencia de inferencia adicional del cálculo separado de los deltas, podríamos modificar el modelo authentic agregando los deltas estimados a sus parámetros. Usamos el add_ Método para modificar el peso in situ.
with_no_grad({
mannequin$weight$add_(delta_theta$t())
})Ahora, aplicar el modelo base a los datos de la nueva distribución produce un buen rendimiento, por lo que podemos decir que el modelo está adaptado para la nueva tarea.
nnf_mse_loss(mannequin(X2), y2)
#> torch_tensor
#> 0.00130013
#> [ CPUFloatType{} ]Concluyendo
Ahora que hemos aprendido cómo funciona LoRA para este ejemplo easy, podemos pensar cómo podría funcionar en modelos grandes previamente entrenados.
Resulta que los modelos de Transformers son en su mayoría una organización inteligente de estas multiplicaciones de matrices, y aplicar LoRA solo a estas capas es suficiente para reducir en gran medida el costo de ajuste fino y al mismo tiempo obtener un buen rendimiento. Puedes ver los experimentos en el artículo de LoRA.
Por supuesto, la thought de LoRA es lo suficientemente easy como para que pueda aplicarse no sólo a capas lineales. Puede aplicarlo a convoluciones, incrustar capas y, de hecho, a cualquier otra capa.
Imagen de Hu et al en el papel LoRA


