TLDR: Proponemos el robustez certificada asimétrica problema, que requiere robustez certificada para una sola clase y refleja escenarios adversarios del mundo actual. Esta configuración enfocada nos permite introducir clasificadores de características convexas, que producen radios certificados deterministas y de forma cerrada del orden de milisegundos.

Figura 1. Ilustración de clasificadores de características convexas y su certificación para entradas de clases sensibles. Esta arquitectura compone un mapa de características continuo de Lipschitz $varphi$ con una función convexa aprendida $g$. Dado que $g$ es convexo, su plano tangente en $varphi(x)$ lo subestima globalmente, lo que produce bolas de norma certificadas en el espacio de características. Lipschitzness de $varphi$ produce certificados escalados adecuadamente en el espacio de entrada authentic.
A pesar de su uso generalizado, los clasificadores de aprendizaje profundo son muy vulnerables a ejemplos contradictorios: pequeñas perturbaciones de imágenes imperceptibles para los humanos que engañan a los modelos de aprendizaje automático para que clasifiquen erróneamente la entrada modificada. Esta debilidad socava gravemente la confiabilidad de los procesos críticos para la seguridad que incorporan el aprendizaje automático. Se han propuesto muchas defensas empíricas contra las perturbaciones adversas, a menudo para luego ser derrotadas por estrategias de ataque más fuertes. Por lo tanto nos centramos en clasificadores certificablemente robustosque proporcionan una garantía matemática de que su predicción permanecerá constante para una bola regular $ell_p$ alrededor de una entrada.
Los métodos de robustez certificados convencionales presentan una serie de inconvenientes, entre los que se incluyen el no determinismo, la ejecución lenta, el escalamiento deficiente y la certificación frente a una sola norma de ataque. Sostenemos que estos problemas pueden abordarse refinando el problema de robustez certificada para que esté más alineado con entornos prácticos de confrontación.
El problema de la robustez certificada asimétrica
Los clasificadores certificablemente robustos actuales producen certificados para insumos que pertenecen a cualquier clase. Para muchas aplicaciones adversas del mundo actual, esto es innecesariamente amplio. Considere el caso ilustrativo de alguien que redacta un correo electrónico fraudulento de phishing mientras intenta evitar los filtros de spam. Este adversario siempre intentará engañar al filtro de spam haciéndole creer que su correo electrónico no deseado es benigno, nunca al revés. En otras palabras, el atacante únicamente intenta inducir falsos negativos del clasificador. Configuraciones similares incluyen detección de malware, señalización de noticias falsas, detección de bots en redes sociales, filtrado de reclamaciones de seguros médicos, detección de fraude financiero, detección de sitios net de phishing y muchas más.
Figura 2. Robustez asimétrica en el filtrado de correo electrónico. Los entornos prácticos de confrontación a menudo requieren solidez certificada para una sola clase.
Todas estas aplicaciones implican una configuración de clasificación binaria con uno clase wise que un adversario intenta evitar (por ejemplo, la clase de “correo electrónico no deseado”). Esto motiva el problema de robustez certificada asimétricacuyo objetivo es proporcionar predicciones sólidas y certificables para entradas de la clase wise y, al mismo tiempo, mantener una precisión alta y limpia para todas las demás entradas. Proporcionamos un planteamiento del problema más formal en el texto principal.
Clasificadores de características convexas
Proponemos redes neuronales de características convexas para abordar el problema de la robustez asimétrica. Esta arquitectura compone un mapa de características continuo de Lipschitz easy ${varphi: mathbb{R}^d to mathbb{R}^q}$ con una crimson neuronal convexa de entrada (ICNN) ${g: mathbb {R}^q to mathbb{R}}$ (Figura 1). Las ICNN imponen la convexidad desde la entrada al logit de salida componiendo no linealidades ReLU con matrices de peso no negativas. Dado que una región de decisión binaria de ICNN consta de un conjunto convexo y su complemento, agregamos el mapa de características precompuesto $varphi$ para permitir regiones de decisión no convexas.
Los clasificadores de características convexas permiten el cálculo rápido de radios certificados de clase wise para todas las normas $ell_p$. Utilizando el hecho de que las funciones convexas están globalmente subestimadas por cualquier plano tangente, podemos obtener un radio certificado en el espacio de características intermedio. Luego, Lipschitzness propaga este radio al espacio de entrada. La configuración asimétrica aquí es basic, ya que esta arquitectura solo produce certificados para la clase logit positiva $g(varphi(x)) > 0$.
La fórmula resultante del radio certificado $ell_p$-norm es particularmente elegante:
[r_p(x) = frac{ color{blue}{g(varphi(x))} } { mathrm{Lip}_p(varphi) color{red}{| nabla g(varphi(x)) | _{p,*}}}.]
Los términos no constantes son fácilmente interpretables: el radio aumenta proporcionalmente a la confianza del clasificador e inversamente a la sensibilidad del clasificador. Evaluamos estos certificados en una variedad de conjuntos de datos, logrando certificados $ell_1$ competitivos y certificados $ell_2$ y $ell_{infty}$ comparables, a pesar de que otros métodos generalmente se adaptan a una norma específica y requieren órdenes de magnitud más tiempo de ejecución. .
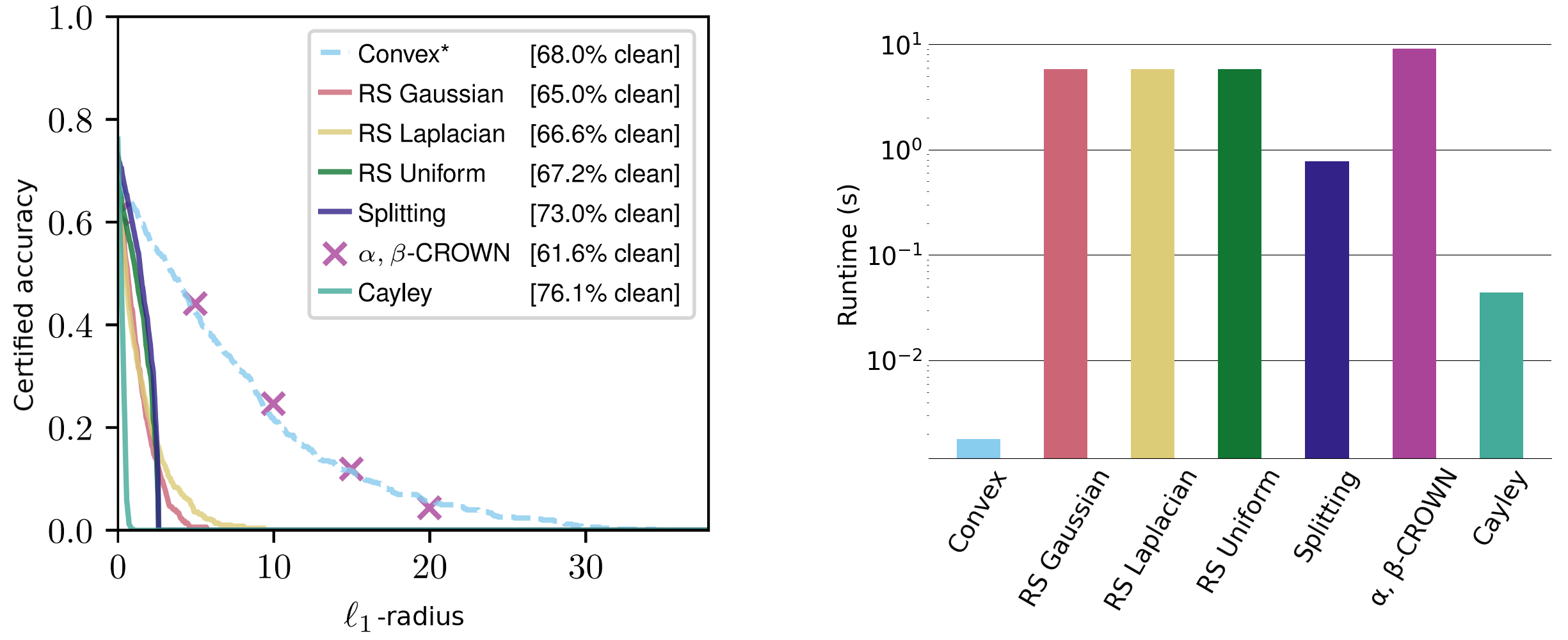
Figura 3. Radios certificados de clase wise en el conjunto de datos de perros y gatos CIFAR-10 para la norma $ell_1$. Los tiempos de ejecución de la derecha se promedian sobre radios $ell_1$, $ell_2$ y $ell_{infty}$ (tenga en cuenta la escala logarítmica).
Nuestros certificados son válidos para cualquier norma $ell_p$ y son de forma cerrada y deterministas, y requieren solo un paso hacia adelante y hacia atrás por entrada. Estos son computables en el orden de milisegundos y se adaptan bien al tamaño de la crimson. A modo de comparación, los métodos actuales de última generación, como el suavizado aleatorio y la propagación limitada por intervalos, suelen tardar varios segundos en certificar incluso redes pequeñas. Los métodos de suavizado aleatorio también son inherentemente no deterministas, con certificados que simplemente se cumplen con una alta probabilidad.
Promesa teórica
Si bien los resultados iniciales son prometedores, nuestro trabajo teórico sugiere que existe un importante potencial sin explotar en las ICNN, incluso sin un mapa de características. A pesar de que las ICNN binarias están restringidas al aprendizaje de regiones de decisión convexas, demostramos que existe una ICNN que logra una precisión de entrenamiento perfecta en el conjunto de datos de perros contra gatos CIFAR-10.
Hecho. Existe un clasificador de entrada convexo que logra una precisión de entrenamiento perfecta para el conjunto de datos de gatos versus perros CIFAR-10.
Sin embargo, nuestra arquitectura logra una precisión de entrenamiento de solo $73,4%$ sin un mapa de características. Si bien el rendimiento del entrenamiento no implica una generalización del conjunto de pruebas, este resultado sugiere que las ICNN son, al menos teóricamente, capaces de alcanzar el paradigma moderno de aprendizaje automático de sobreajuste al conjunto de datos de entrenamiento. Planteamos así el siguiente problema abierto para el campo.
Problema abierto. Aprenda un clasificador de entrada convexo que logra una precisión de entrenamiento perfecta para el conjunto de datos de gatos versus perros CIFAR-10.
Conclusión
Esperamos que el marco de robustez asimétrica encourage arquitecturas novedosas que sean certificables en este entorno más centrado. Nuestro clasificador de características convexas es una de esas arquitecturas y proporciona radios certificados rápidos y deterministas para cualquier norma $ell_p$. También planteamos el problema abierto de sobreajustar el conjunto de datos de entrenamiento de perros y gatos CIFAR-10 con una ICNN, lo que demostramos que es teóricamente posible.
Esta publicación se basa en el siguiente artículo:
Robustez certificada asimétrica a través de redes neuronales convexas
Samuel Pfrommer,
Brendon G.Anderson,
Julien Piet,
Somayeh Sojoudi,
37ª Conferencia sobre Sistemas de Procesamiento de Información Neural (NeurIPS 2023).
Más detalles están disponibles en arXiv y GitHub. Si nuestro artículo inspira su trabajo, considere citarlo con:
@inproceedings{
pfrommer2023asymmetric,
title={Uneven Licensed Robustness by way of Characteristic-Convex Neural Networks},
creator={Samuel Pfrommer and Brendon G. Anderson and Julien Piet and Somayeh Sojoudi},
booktitle={Thirty-seventh Convention on Neural Data Processing Techniques},
12 months={2023}
}


